LINKED PAPER
Quantifying the maculation of avian eggs using eggshell geometry. Pike, T. W. 2019. IBIS. DOI: 10.1111/ibi.12708. VIEW
Bird eggs are often decorated by beautiful and intricate pigmentation patterns, from casual blotches to zigzagging lines. The exact function of these patterns – which ornithologists call maculation – is still uncertain. Several hypotheses have been proposed (Kilner 2006, Cassey et al. 2011), such camouflage to avoid predation, thermoregulation and defense against bacterial infections. To test this panoply of ideas, scientists need to quantify the maculation patterns and that is more difficult than it seems.
Curvature
Typically, researchers rely on photographs of eggs to take their measurements. However, this approach assumes that the egg surface is flat. And that is obviously not the case. The linear distance between two points on the picture will be shorter than the actual difference due to the curvature of the egg. This situation is similar to the familiar map of the world that might be adorning your office wall. On some two-dimensional versions of this map Greenland seems to be half the size of Africa. In reality, however, Africa is about 14 times bigger than Greenland. The curvature of the Earth stretches the dimensions of the African continent if you would wrap the map around a globe. The same principle applies to eggs as shown by the figure below.
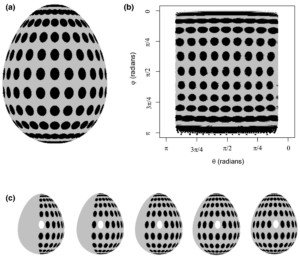
Figure 1 Measuring pigmentation patterns on a three-dimensional object can be challenging. Transferring the patterns from the picture of an egg (a) to a two-dimensional surface (b) seems to show that the black circles are different. However, the circles are exactly the same size (c) but become distorted due to the curvature of the egg.
Divide and calculate
Thomas Pike from the University of Lincoln devised a mathematical method to account for this curvature when measuring maculation. To determine the shortest distance between two points on a curved surface, you can divide the path between these points into small segments. The smaller the segments, the less influence curvature has on the measurement. The sum of all these short distances gives a reliable approximation of the actual distance. This approach can also be used to measure surfaces, for example the size of a black blotch on an Oystercatcher (Haematopus ostralegus) egg. Instead of smaller sections of a line, you now divide the surface into smaller and smaller triangles. In the end, just sum up the surfaces of these tiny triangles.
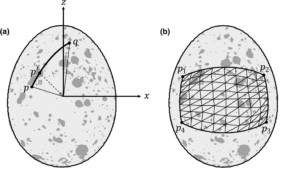
Figure 2 You can measure the distance between two points on a curved surface by dividing the path into smaller sections (a). The same approach can be used to quantify a surface area. Divide the area into tiny triangles and sum up their surfaces (b).
Shapes
Bird eggs come in a wide variety of shapes (Stoddard et al. 2017). The method outlined above can easily applied to all kinds of curving surfaces, from the almost spherical eggs of the Brown Hawk-owl (Ninox scutulata) to the pointed eggs of the Common Guillemot (Uria aalge). There are several other ways to quantify maculation (Baker 2002, Ornés et al. 2014). Together, these methods might uncover the functional relevance of pigmentation patterns on bird eggs.
References
Baker, D. E. 2002. A geometric method for determining shape of bird eggs. The Auk 119: 1179-1186. VIEW
Cassey, P., Maurer, G., Lovell, P. G. & Hanley, D. 2011. Conspicuous eggs and colourful hypotheses: testing the role of multiple influences on avian eggshell appearance. Avian Biology Research 4: 185-195. VIEW
Kilner, R. M. 2006. The evolution of egg colour and patterning in birds. Biological Reviews 81: 383-406. VIEW
Ornés, A. S., Herbst, A., Spillner, A., Mewes, W. & Rauch, M. 2014. A standardized method for quantifying eggshell spot patterns. Journal of Field Ornithology 85: 397-407. VIEW
Stoddard, M. C., Yong, E. H., Akkaynak, D., Sheard, C., Tobias, J. A., & Mahadevan, L. 2017. Avian egg shape: Form, function, and evolution. Science 356: 239-243. VIEW
Image credits
Featured image: Eggs of a Spotted Crake Porzana porzana | Roger Culos | CC BY-SA 4.0 Wikimedia Commons




